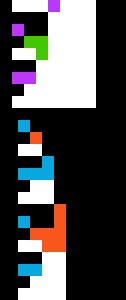bitmap-editor/tools/bitmap editor/apple2_hires.md

Revisiting Apple ][ hires

Summary

• Introduction
• Structure of the hires screen in RAM
• Summary table of addresses in RAM
• Taking advantage of the hires structure
  • Use case #1: displaying tiles
  • Use case #2: clearing the screen
  • Use case #3: side-scrolling
• Hires colors: some possibilities, lots of limitations
  • Hires rules part 1: first limitations
  • Hires rules part 2: more limitations
  • Hires rules part 3: more colors but more limitations
  • Hires rules part 4: is that 560 pixels horizontally ?

Introduction

A lot has been said and written on the Apple ][ hires screens. How colors work, how it's organized in RAM, how to animate sprites, how to clear the screen faster than the HGR/HGR2 Applesoft commands, how to draw faster lines than HPLOT, etc.

This article does not have the pretention to uncover anything new regarding hires pages: if you know how to program your Apple ][ then most of the information here will be old news to you. Nonetheless there might be a trick or two that I learned the hard way that still might be useful to you.

I've written this as if you didn't know much about hires on Apple ][ except maybe a few Applesoft commands like HGR/HGR2, HCOLOR and HPLOT. Maybe even DRAW/XDRAW ... and yet you don't know how it works behind all this.

So this article will first cover the basics: structure of the hires pages in RAM, pixels and colors (even in those sections you might find some rare info) and then will dive into specific techniques and tools I've encountered or developed.

I'll try to make you understand how it works by using Applesoft most of the time, so I expect you know mostly how to program in Applesoft. I won't explain the Applesoft code much except using some REMs in the code.

Some parts of this article will feature 6502 code. If you're not comfortable with 6502, don't worry, just skip the section.

Structure of the hires screen in RAM

The Apple ][ has 2 hires pages. One in $2000-$3FFF. The second one in $4000-$5FFF. Each page is thus 8192 bytes long.

The dimensions of one hires page are 40 bytes wide and 192 lines high. 40x192 = 7680 bytes. 512 bytes are "missing" and in fact not used/displayed.

The hires screen is divided in 3 zones of 64 lines. Let's call it zones A. Each section is then divided in 8 sub-sections of 8 lines. Let's call these zones B. Every B zone is itself divided in 8 sub-sub-sections representing the lines themselves. These are zones C.

To better understand this division, it's easier to POKE bytes into RAM and see what happens.

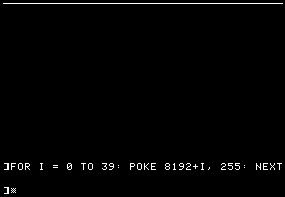
A POKE 8192,255will plot 7 pixels on the top left corner of the hires screen (page 1). Poking the next memory address (8193), will plot 7 more pixels on line 0 of the hires screen.

So to draw the entire line 0 we could RUN this code

10 HGR
20 FOR I = 0 TO 39: POKE 8192+I, 255: NEXT

8192 + 40 = 8232 ($2028) is the next byte in memory. ButPOKE 8232,255 will not plot 7 pixels on line 1 but on line 64 !

If we slightly modify the above code to POKE the first 3 lines as stored in memory, we have

10 HGR
20 P = 8192: REM $2000
30 FOR A = 0 TO 2: REM 3 A-ZONES
40 FOR I = 0 TO 39: REM 40 BYTES PER LINE
50 POKE P, 255
60 P = P + 1
70 NEXT I,A
80 PRINT P

The result is this

We have drawn line 0, line 64 and line 128 ! These 3 lines represent the first line of each A-zone.

Now the next address to POKE seems to be 8312 ($2078 in hex -- the resulting value in our variable P).

But if we do POKE 8312, 255 we don't see any change on the screen ! This is because we have reached one the hires screen holes !

In fact, all lines between 128 and 191 in RAM have 8 unused bytes at their end. Those 8x64 lines represent 512 bytes. Those are the missing bytes in first computation.

Now that we now that, we could slightly modify the above code so that after having drawn 3 lines, we add 8 to Aso that it points to the next line location in memory. Let's do it and plot 3 times 3 lines.

10 HGR
20 P = 8192: REM $2000
30 FOR B = 0 TO 2: REM FOR NOW JUST DRAW INTO 3 B-ZONES
40 FOR A = 0 TO 2: REM 3 A-ZONES
50 FOR I = 0 TO 39: REM 40 BYTES PER LINE
60 POKE P, 255
70 P = P + 1
80 NEXT I,A
90 P = P + 8
100 NEXT B
110 PRINT P

We end up with

As you watch how the lines are filled, you better understand the hires screen structure:

• the first 3 lines of 40 bytes delimit the three A-zones and represent lines 0, 64 and 128 of the screen. Incidentally, these are too the first B-zones of each A-zone.
• then 8 bytes are wasted
• the next 3 lines of 40 bytes represent line 8 of each of the A-zones and the 2nd B-zone of each A-zone (that is the base line of each A-zone + 8, so we have lines 0+8, 64+8 and 128+8)
• then 8 bytes are wasted
• the next 3 lines of 40 bytes represent line 16 of each of the A-zones and the 3rd B-zone in each A-zone
• then 8 bytes are wasted
• This continues until we've arrived at line 56 relative to each A-zone, which is also the 8th B-zone for each A-zone. That is line 0+56=56, line 64+56=120 and line 128+56=184.

The following code will do it

10 HGR
20 P = 8192: REM $2000
30 FOR B = 0 TO 7: REM 8 B-ZONES IN EACH A-ZONE
40 FOR A = 0 TO 2: REM 3 A-ZONES
50 FOR I = 0 TO 39: REM 40 BYTES PER LINE
60 POKE P, 255
70 P = P + 1
80 NEXT I,A
90 P = P + 8
100 NEXT B
110 PRINT A

So what happens next ? Well, a POKE 9216,255 will show you that you're plotting on line 1 ! And once line 1 has been filled, you'll plot on line 65 ! And then on line 129 ! Then back to first section of 64-lines but on line 8+1=9, then on line 16+1=17, etc.

10 HGR
20 P = 8192: REM $2000
30 FOR C = 0 TO 7: REM 8 C-ZONES IN EACH B-ZONE
40 FOR B = 0 TO 7: REM 8 B-ZONES IN EACH A-ZONE
50 FOR A = 0 TO 2: REM 3 A-ZONES
60 FOR I = 0 TO 39: REM 40 BYTES PER LINE
70 POKE P, 255
80 P = P + 1
90 NEXT I,A
100 P = P + 8
110 NEXT B,C
120 PRINT P

If you run the above code, your screen will be filled and A will point to 16384 (or $4000) which is the start of page 2.

To sum it up, the logical structure of the line numbers in RAM is as follows:

1. There are 3 sections of 64 lines beginning at lines 0, 64 and 128. The baseline of the A-zones.
2. The baseline for the C-zones is set to zero
3. The baseline for the B-zones is set to zero
4. The baseline for the A-zone is set to zero
5. RAM holds the line = (A-zone baseline) + (B-zone baseline) + (C-zone baseline)
6. Baseline for the A-zone is incremented by 64
7. Back to step 5, two more times
8. Then 8 bytes are wasted
9. B-zone baseline is incremented by 8
10. Back to step 4, seven more times
11. C-zone baseline is incremented by 1
12. Back to step 3, seven more times

In code that would be

10 HGR: P = 8192
20 C = 0 : NC = 0 : REM C-ZONE BASELINE AND COUNTER
30 B = 0 : NB = 0 : REM B-ZONE BASELINE AND COUNTER
40 A = 0 : NA = 0 : REM A-ZONE BASELINE AND COUNTER
50 HPLOT 0, A + B + C TO 279, A + B + C: REM DRAW A WHOLE LINE
60 PRINT A + B + C;": ";P" ";: A = A + 64: P = P + 40: REM INCREMENT A-ZONE BASELINE AND POINTER P
70 NA = NA + 1 : IF NA < 3 THEN GOTO 50: REM THERE ARE 3 A-ZONES
80 P = P + 8: REM HERE 8 BYTES ARE NOT USED
90 B = B + 8: REM INCREMENT B-ZONE BASELINE
100 NB = NB + 1: IF NB<8 THEN GOTO 40: REM 8 B-ZONES PER A-ZONE
110 C = C + 1
120 NC = NC + 1: IF NC<8 THEN GOTO 30: REM 8 C-ZONES PER B-ZONE

Notice how the HPLOTs draw the lines in the same order as the POKEs in the previous programs.

The starting address of a line Y in hires page 1 is found using the following formula:

A = INT(Y/64): REM A-ZONE
B = INT( (Y - 64 * A) / 8): REM B-ZONE
C = INT(Y - 64 * A - 8 * B): REM C-ZONE
P = 8192 + A * 40 + B * 128 + C * 1024: REM STARTING ADDRESS IN RAM

Summary table of addresses in RAM

Here are all the addresses for hires page 1. Simply add #$40 to all MSB for page 2.

Line	Start	End	Line	Start	End	Line	Start	End	Line	Start	End	Line	Start	End	Line	Start	End	Line	Start	End	Line	Start	End
0	$2000	$2027	1	$2400	$2427	2	$2800	$2827	3	$2C00	$2C27	4	$3000	$3027	5	$3400	$3427	6	$3800	$3827	7	$3C00	$3C27
64	$2028	$204F	65	$2428	$244F	66	$2828	$284F	67	$2C28	$2C4F	68	$3028	$304F	69	$3428	$344F	70	$3828	$384F	71	$3C28	$3C4F
128	$2050	$2077	129	$2450	$2477	130	$2850	$2877	131	$2C50	$2C77	132	$3050	$3077	133	$3450	$3477	134	$3850	$3877	135	$3C50	$3C77
wasted	$2078	$207F	wasted	$2478	$247F	wasted	$2878	$287F	wasted	$2C78	$2C7F	wasted	$3078	$307F	wasted	$3478	$347F	wasted	$3878	$387F	wasted	$3C78	$3C7F
8	$2080	$20A7	9	$2480	$24A7	10	$2880	$28A7	11	$2C80	$2CA7	12	$3080	$30A7	13	$3480	$34A7	14	$3880	$38A7	15	$3C80	$3CA7
72	$20A8	$20CF	73	$24A8	$24CF	74	$28A8	$28CF	75	$2CA8	$2CCF	76	$30A8	$30CF	77	$34A8	$34CF	78	$38A8	$38CF	79	$3CA8	$3CCF
136	$20D0	$20F7	137	$24D0	$24F7	138	$28D0	$28F7	139	$2CD0	$2CF7	140	$30D0	$30F7	141	$34D0	$34F7	142	$38D0	$38F7	143	$3CD0	$3CF7
wasted	$20F8	$20FF	wasted	$24F8	$24FF	wasted	$28F8	$28FF	wasted	$2CF8	$2CFF	wasted	$30F8	$30FF	wasted	$34F8	$34FF	wasted	$38F8	$38FF	wasted	$3CF8	$3CFF
16	$2100	$2127	17	$2500	$2527	18	$2900	$2927	19	$2D00	$2D27	20	$3100	$3127	21	$3500	$3527	22	$3900	$3927	23	$3D00	$3D27
80	$2128	$214F	81	$2528	$254F	82	$2928	$294F	83	$2D28	$2D4F	84	$3128	$314F	85	$3528	$354F	86	$3928	$394F	87	$3D28	$3D4F
144	$2150	$2177	145	$2550	$2577	146	$2950	$2977	147	$2D50	$2D77	148	$3150	$3177	149	$3550	$3577	150	$3950	$3977	151	$3D50	$3D77
wasted	$2178	$217F	wasted	$2578	$257F	wasted	$2978	$297F	wasted	$2D78	$2D7F	wasted	$3178	$317F	wasted	$3578	$357F	wasted	$3978	$397F	wasted	$3D78	$3D7F
24	$2180	$21A7	25	$2580	$25A7	26	$2980	$29A7	27	$2D80	$2DA7	28	$3180	$31A7	29	$3580	$35A7	30	$3980	$39A7	31	$3D80	$3DA7
88	$21A8	$21CF	89	$25A8	$25CF	90	$29A8	$29CF	91	$2DA8	$2DCF	92	$31A8	$31CF	93	$35A8	$35CF	94	$39A8	$39CF	95	$3DA8	$3DCF
152	$21D0	$21F7	153	$25D0	$25F7	154	$29D0	$29F7	155	$2DD0	$2DF7	156	$31D0	$31F7	157	$35D0	$35F7	158	$39D0	$39F7	159	$3DD0	$3DF7
wasted	$21F8	$21FF	wasted	$25F8	$25FF	wasted	$29F8	$29FF	wasted	$2DF8	$2DFF	wasted	$31F8	$31FF	wasted	$35F8	$35FF	wasted	$39F8	$39FF	wasted	$3DF8	$3DFF
32	$2200	$2227	33	$2600	$2627	34	$2A00	$2A27	35	$2E00	$2E27	36	$3200	$3227	37	$3600	$3627	38	$3A00	$3A27	39	$3E00	$3E27
96	$2228	$224F	97	$2628	$264F	98	$2A28	$2A4F	99	$2E28	$2E4F	100	$3228	$324F	101	$3628	$364F	102	$3A28	$3A4F	103	$3E28	$3E4F
160	$2250	$2277	161	$2650	$2677	162	$2A50	$2A77	163	$2E50	$2E77	164	$3250	$3277	165	$3650	$3677	166	$3A50	$3A77	167	$3E50	$3E77
wasted	$2278	$227F	wasted	$2678	$267F	wasted	$2A78	$2A7F	wasted	$2E78	$2E7F	wasted	$3278	$327F	wasted	$3678	$367F	wasted	$3A78	$3A7F	wasted	$3E78	$3E7F
40	$2280	$22A7	41	$2680	$26A7	42	$2A80	$2AA7	43	$2E80	$2EA7	44	$3280	$32A7	45	$3680	$36A7	46	$3A80	$3AA7	47	$3E80	$3EA7
104	$22A8	$22CF	105	$26A8	$26CF	106	$2AA8	$2ACF	107	$2EA8	$2ECF	108	$32A8	$32CF	109	$36A8	$36CF	110	$3AA8	$3ACF	111	$3EA8	$3ECF
168	$22D0	$22F7	169	$26D0	$26F7	170	$2AD0	$2AF7	171	$2ED0	$2EF7	172	$32D0	$32F7	173	$36D0	$36F7	174	$3AD0	$3AF7	175	$3ED0	$3EF7
wasted	$22F8	$22FF	wasted	$26F8	$26FF	wasted	$2AF8	$2AFF	wasted	$2EF8	$2EFF	wasted	$32F8	$32FF	wasted	$36F8	$36FF	wasted	$3AF8	$3AFF	wasted	$3EF8	$3EFF
48	$2300	$2327	49	$2700	$2727	50	$2B00	$2B27	51	$2F00	$2F27	52	$3300	$3327	53	$3700	$3727	54	$3B00	$3B27	55	$3F00	$3F27
112	$2328	$234F	113	$2728	$274F	114	$2B28	$2B4F	115	$2F28	$2F4F	116	$3328	$334F	117	$3728	$374F	118	$3B28	$3B4F	119	$3F28	$3F4F
176	$2350	$2377	177	$2750	$2777	178	$2B50	$2B77	179	$2F50	$2F77	180	$3350	$3377	181	$3750	$3777	182	$3B50	$3B77	183	$3F50	$3F77
wasted	$2378	$237F	wasted	$2778	$277F	wasted	$2B78	$2B7F	wasted	$2F78	$2F7F	wasted	$3378	$337F	wasted	$3778	$377F	wasted	$3B78	$3B7F	wasted	$3F78	$3F7F
56	$2380	$23A7	57	$2780	$27A7	58	$2B80	$2BA7	59	$2F80	$2FA7	60	$3380	$33A7	61	$3780	$37A7	62	$3B80	$3BA7	63	$3F80	$3FA7
120	$23A8	$23CF	121	$27A8	$27CF	122	$2BA8	$2BCF	123	$2FA8	$2FCF	124	$33A8	$33CF	125	$37A8	$37CF	126	$3BA8	$3BCF	127	$3FA8	$3FCF
184	$23D0	$23F7	185	$27D0	$27F7	186	$2BD0	$2BF7	187	$2FD0	$2FF7	188	$33D0	$33F7	189	$37D0	$37F7	190	$3BD0	$3BF7	191	$3FD0	$3FF7

Taking advantage of the hires structure

This structure might seem confusing and it's true that most of the time programmers will use lookup tables to find the starting address of a line instead of using the above formula.

Nonetheless, even such an interlaced structure could be used without resorting systematically to lookup tables, depending on the use case.

Use case #1: displaying tiles

For example, if we're on a line that's a multiple of 8 (that's the first 3 columns in the table above), all we have to do to find the address of the next 8 lines is to add 4 to the most significant byte (MSB) of the address. In 6502 that's only one instruction (after you've cleared the carry), which might be cycle-saving. In Applesoft it means adding 1024 to the base address.

For instance, if we draw bitmaps starting from a line that is a multiple of 8, like it might be the case when displaying 8-lines high tiles in a game , we only need the address of the first line, while the address of the other lines have the same LSB but an MSB that is incremented by four each time.

Use case #2: clearing the screen

Another example is when you write a fast routine to clear the hires screen. You'll want to skip the hires holes for two reasons:

1. It's 512 bytes that don't need to be cleared and that will waste cycles
2. You may want to use these 512 bytes to store data and so you don't want to erase it

The position of the screen holes is also very regular. First they are all within the third section of the screen. Then their address range is either $xx78-$xx7F or $xxF8-$xxFF.

We make use of this information by looping down from #$F7 (thus skipping the second kind of hole area) to #$00 but skipping to #$77 once we reach #$7F.

Use case #3: side-scrolling

If you closely watch the above table, you'll notice that the last A-zone starting addresses all end with either $xx50 or $xxD0. It means that if you want to address this zone, all you have to do is cycle from #$20 to #$3F for the MSB and flip between #$50 and #$D0 for the LSB, for instance by using an EOR #$80.

This could be used for instance in a game where the screen scrolls only on the lower third of the screen. You know, in airplanes fighting games, this is usually where the ground and the enemies are (hint, hint).

The same is in fact true the other two A-zones. For the first one, addresses end with either $00 or $80. For the second one, it's $28 and $A8. But maybe the use cases are less obvious ?

Now imagine you want scroll only the last 32 lines of the screen, then the MSB of the baseline will be either #$22 or #$23 to which you add 4 for each of the next seven lines while the LSB flips between #$50 and #$D0. And you have many options to unroll the loops if you want to speed things up a little bit further.

For instance this code would copy bytes 1-39 of each line of the 32 last lines of the screen to bytes 0-38 effectively scrolling that part of the screen one byte to the left.

(Note: this is just one way, I'm not saying it's better than any other)

	LDA #$22			; base address MSB
            
.loopx  SEC				; set carry
	STA .ldy1+2			; self modifying code
	STA .sty1+2			; MSB for first 2 lines
	STA .ldy2+2
	STA .sty2+2
	ADC #0				; 0+carry = 1 !
	STA .ldy3+2			; MSB of the last 2 lines
	STA .sty3+2			; add one more for the
	STA .ldy4+2
	STA .sty4+2
	TAY				; save in Y for now
            
		
	LDX #0				; init byte counter
.loop					; 4 lines at a time
.ldy1	LDA $2251,X			; copy byte X on 1st line
.sty1	STA $2250,X			; to previous byte
.ldy2	LDA $22D1,X			; same for 2nd line
.sty2	STA $22D0,X
.ldy3	LDA $2351,X			; 3rd line
.sty3	STA $2350,X
.ldy4	LDA $23D1,X			; 4th line
.sty4	STA $23D0,X
	INX				; next byte
	CPX #$27			; last byte ?
	BCC .loop			; not yet
	TYA				; carry is set ! get back MSB
	ADC #2				; 2+carry = 3 !
	CMP #$40			; have we done them all ?
	BCC .loopx			; not yet
	

Hires colors: some possibilities, lots of limitations

So far we've been filling the screen with blocks of 7 pixels. How comes one byte, which is 8 bits, is only 7 pixels on the screen ?

To understand this, the best way is to go back to basics and to BASIC !

Let's try this (don't forget to type NEW beforehand)

10 HGR
20 FOR Y = 0 TO 127
30 A = INT(Y/64): REM A-ZONE
40 B = INT( (Y - 64 * A) / 8): REM B-ZONE
50 C = INT(Y - 64 * A - 8 * B): REM C-ZONE
60 P = 8192 + A * 40 + B * 128 + C * 1024: REM STARTING ADDRESS IN RAM
70 POKE P,Y
80 NEXT

Here's the output:

What we've done is POKE values 0-127 into the first bytes of the first 128 lines of the hires screen.

The results are very informative. Let's zoom in a bit.

The first line of pixels is black, corresponding to 0. POKEing 1 in the next line produced a violet dot in x=0, while POKEing 2 resulted in a green dot in x=1 and finally, POKEing 3 created two white dots, one in position 0 and the other in position 1.

Hires rules part 1: first limitations

From these 4 POKE, we can already see that

1. Plotting is inverted compared to the order of the representation of a binary value.

dec	binary	result
0	000	black-black-black
1	001	violet-black-black
2	010	black-green-black
3	011	white-white-black

2. Violet pixels are on even columns while green pixels are on odd columns.

3. White pixels are always grouped by 2 or more pixels

4. Except on the edges of the screen, the same is true for black pixels

5. A black pixel surrounded by two others will be rendered using the color of one of the two other pixels, but NEVER white

To understand what color a pixel is going to be rendered, one must consider the pixel on both sides of the considered pixel.

even	odd	even	pixel n is
pixel n-1	pixel n	pixel n+1	rendered as
off	off	off	black
off	off	on	black
on	off	off	black
on	off	on	color of even column
off	on	off	color of odd column
off	on	on	white
on	on	off	white
on	on	on	white

This might be summarised as the following:

• if the pixel is off, it's rendered black except if both its neighbours are on, in which case it's rendered using the color of its neighbours' columns
• if the pixel is on, it's rendered white except if both its neighbours are off, in which cas it's rendered using the color of his own column.

Hires rules part 2: more limitations

And we can continue our observations:

6. It's impossible to plot more than one pair of consecutive colored pixels: colored pixels are always odd in number

7. To plot only two consecutive colored pixels, they must be surrounded by two white pixels on one side and two black pixels on the other side

8. Single dot (then colored) pixels must be surrounded by two pairs of black pixels but the minimum distance between two single dot pixels of the same color is 3 black pixels. The minimum distance between two single dot pixels of different colors is 2 pixels.

Hires rules part 3: more colors but more limitations

Now what about values above 128 ? Let's edit line 20 of the previous program

20 FOR Y = 0 TO 160

Yes ! New colors !

So, the 7th bit switches to a different color palette. Pixels in this palette follow the same rules as the previous palette. But we can add more observations.

9. A second palette is selected when the 7th bit (AKA the "hi-bit") is ON

10. Blue is on even columns and orange/red is on odd columns ... HEY WAIT !! LOOK CLOSELY !

Hires rules part 4: is that 560 pixels horizontally ?

11. Blue pixels are displayed in-between the columns of the violet/green pixels while red pixels are displayed in-between the columns of the green/violet pixels.

How weird is that ? Let's try this:

10 HGR: N=128: YY=0
20 FOR Y = 0 TO 127
30 A = INT(Y/64): REM A-ZONE
40 B = INT( (Y - 64 * A) / 8): REM B-ZONE
50 C = INT(Y - 64 * A - 8 * B): REM C-ZONE
60 P = 8192 + A * 40 + B * 128 + C * 1024: REM STARTING ADDRESS IN RAM
70 POKE P,YY+N
80 N = 128-N: IF N=0 THEN YY=YY+1
90 NEXT

What this does is plotting increasing values but every other line we add 128 to see the equivalent of the second palette.

As you can see, not only are the color pixels of the other palette slightly shifted but the whites and blacks too !

Ok, let's try something else using HPLOT and HCOLOR this time ..

NEW
10 HGR
20 X=0: C = 3
30 FOR Y = 0 TO 159
40 HCOLOR = C
50 HPLOT X,Y
60 C=10-C
70 IF C = 3 THEN X=X+1
90 NEXT

What a beautiful colored line ... looks so sharp !

What we did was plot one dot with the first palette, go down one line, plot a dot with the second palette in the same X-coord, go down one line, plot a dot in the next X-coord with the first palette, and so on.

Let's zoom in

This is why sometimes you can read that the Apple ][ has a hires resolution of 560x192 (and I'm not talking about double hi-res which is an entirely different topic !). It's possible to plot "between" columns of the other palette making it look like the resolution is 560 pixels wide. But practically, this is not useable because on one byte you may activate only one palette (using the 7th bit). So it can be used mostly only if you're turn on only one bit in the 7-pixels byte. Since you need at least 2 black pixels between single dot pixels and that you can't use the "in-between" columns until 7 pixels further, the illusion of 560 pixels horizontally will quickly vanish.

Is the Apple ][ hires screen 280 pixels wide ? Yes, if you consider a monochrome display, it is. If you're counting on colors, it's more like a 140 pixels wide screen since you need two pixels to render white. And as we've seen there are a lot of limitations on the use of colors.

Let's speak of two others ... yes, the nightmare is far from finished !

Hires rules part 5: last but not least

Even and odd bytes have their color bits swapped. Preshifting bitmaps Consecutive bytes with hi-bit set/unset will cause color problems.